5.2 参数管理

要点
  • module.weight 是一个 nn.Parameter 类，可以用（bias 同理）：
    • module.weight.data 查看参数值
    • module.weight.grad 查看参数梯度
  • 参数绑定下的梯度，应该是先当做未绑定的参数，再计算参数梯度结果，矢量相加

用 Sequential 定义具有单隐藏层的多层感知机：

import torch
from torch import nn

net = nn.Sequential(nn.Linear(4, 8), nn.ReLU(), nn.Linear(8, 1))
X = torch.rand(size=(2, 4))
net(X)

1. 参数访问

当通过 Sequential 类定义模型时，我们可以通过索引来访问模型的任意层。这就像模型是一个列表一样，可以取第二个层参数的状态：

print(net[2].state_dict())

注意：这里：

  • net[0] 是 nn.Linear(4, 8)
  • net[1] 是 nn.ReLU()
  • net[2] 是 nn.Linear(8, 1)

也可以访问具体参数：

print(type(net[2].bias))  # <class 'torch.nn.parameter.Parameter'>
print(net[2].bias)        # Parameter containing: tensor([-0.2004], requires_grad=True)
print(net[2].bias.data)   # tensor([-0.2004], requires_grad=True)
print(net[2].bias.grad)   # None （）还没有执行反向传播，梯度初始化就是 None）

有的时候不想索引，而是用名字访问

print(*[(name, param.shape) for name, param in net.named_parameters()])
# ('0.weight', torch.Size([8, 4])) ('0.bias', torch.Size([8])) ('2.weight', torch.Size([1, 8])) ('2.bias', torch.Size([1]))

net.state_dict()['2.bias'].data
# tensor([0.0887])

对于嵌套定义的网络：

def block1():
    return nn.Sequential(nn.Linear(4, 8), nn.ReLU(),
                         nn.Linear(8, 4), nn.ReLU())

def block2():
    net = nn.Sequential()
    for i in range(4):
        # 在这里嵌套
        net.add_module(f'block {i}', block1())
    return net

rgnet = nn.Sequential(block2(), nn.Linear(4, 1))
rgnet(X)

net.add_module ：动态添加网络，参数是网络名 + module

对于简单的嵌套网络，可以 print 查看网络结构：

print(rgnet)

Sequential(
  (0): Sequential(
    (block 0): Sequential(
      (0): Linear(in_features=4, out_features=8, bias=True)
      (1): ReLU()
      (2): Linear(in_features=8, out_features=4, bias=True)
      (3): ReLU()
    )
    (block 1): Sequential(
      (0): Linear(in_features=4, out_features=8, bias=True)
      (1): ReLU()
      (2): Linear(in_features=8, out_features=4, bias=True)
      (3): ReLU()
    )
    (block 2): Sequential(
      (0): Linear(in_features=4, out_features=8, bias=True)
      (1): ReLU()
      (2): Linear(in_features=8, out_features=4, bias=True)
      (3): ReLU()
    )
    (block 3): Sequential(
      (0): Linear(in_features=4, out_features=8, bias=True)
      (1): ReLU()
      (2): Linear(in_features=8, out_features=4, bias=True)
      (3): ReLU()
    )
  )
  (1): Linear(in_features=4, out_features=1, bias=True)
)

我们也可以像通过嵌套列表索引一样访问它们：

rgnet[0][1][0].bias.data

2. 参数初始化

2. 1 内置初始化

下面的代码将所有权重参数初始化为标准差为0.01的高斯随机变量，且将偏置参数设置为0

def init_normal(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, mean=0, std=0.01)
        nn.init.zeros_(m.bias)
net.apply(init_normal)
net[0].weight.data[0], net[0].bias.data[0]
`nn.init.normal_`、`nn.init.zeros_`

带下划线的函数都是原地更新，参考 [[2.1 数据操作#^d365bf]]

`net.apply`

是一个用于递归地应用函数到每一个子模块（包括自己）的 PyTorch 方法，所以在初始化的时候加上 if type(m) == nn.Linear: 是为了确保初始化到最小网络单元

对于自定义类，其 type 是 自定义类名，例如：

class CustomLayer(nn.Module):
    def __init__(self):
        super().__init__()
        self.net = nn.Linear(10, 10)

    def forward(self, x):
        return self.net(x)  
custom_net = CustomLayer()
type(custom_net) == CustomLayer # True

也可以对不同的层级用不同的初始化：

def init_xavier(m):
    if type(m) == nn.Linear:
        nn.init.xavier_uniform_(m.weight)
def init_42(m):
    if type(m) == nn.Linear:
        nn.init.constant_(m.weight, 42)

net[0].apply(init_xavier)
net[2].apply(init_42)
print(net[0].weight.data[0])
print(net[2].weight.data)

nn.init.constant_ 最好不这样初始化，因为初始化要打破参数对称性（参考4.8 数值稳定性和模型初始化#^1537f9）

2.2 自定义初始化

也可以自己设置初始化，参数初始化写到 __init__ 里：

def my_init(m):
    if type(m) == nn.Linear:
        print("Init", *[(name, param.shape)
                        for name, param in m.named_parameters()][0])
        nn.init.uniform_(m.weight, -10, 10)
        m.weight.data *= m.weight.data.abs() >= 5

net.apply(my_init)
net[0].weight[:2]

3. 参数绑定

有时候网络需要完全相同的参数，它们不仅值相等，而且是同一对象（改变其中参数大小，一个另一个也会发生变化），例如：

# 我们需要给共享层一个名称，以便可以引用它的参数
shared = nn.Linear(8, 8)
net = nn.Sequential(nn.Linear(4, 8), nn.ReLU(),
                    shared, nn.ReLU(),
                    shared, nn.Sigmoid(),
                    nn.Linear(8, 1))
net(X)
# 检查参数是否相同
print(net[2].weight.data[0] == net[4].weight.data[0])
net[2].weight.data[0, 0] = 100
# 确保它们实际上是同一个对象，而不只是有相同的值
print(net[2].weight.data[0] == net[4].weight.data[0])

理解参数绑定下的反向传播 ：

下面是一个简单示例，假设网络结构是 nn.Sequential(nn.Linear(1, 1),nn.Linear(1, 1)):

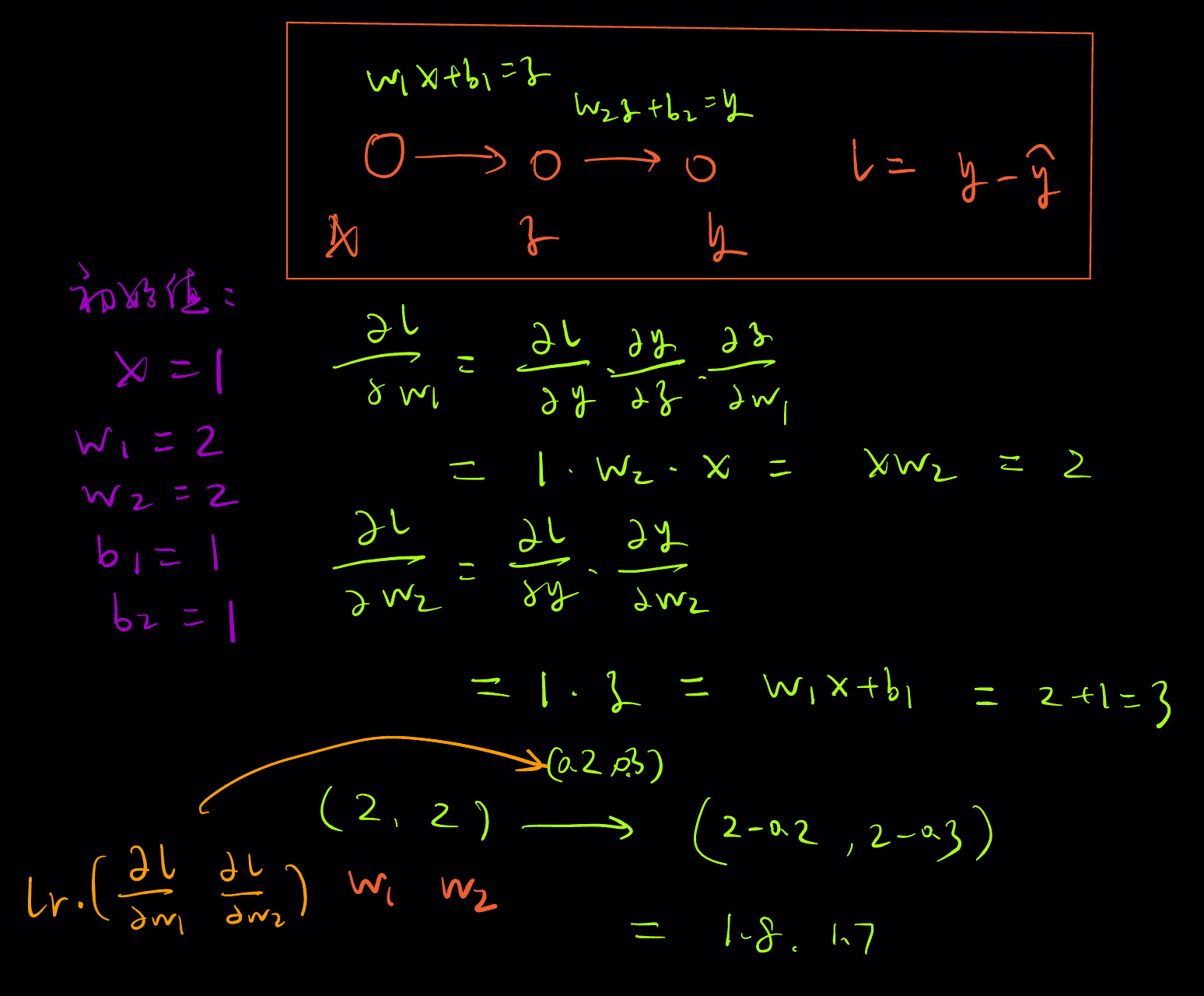
5.2 参数管理-2.png|center|600 一个最简单的一元神经网络，可以通过代码验证计算结果 （代码如下）

class ParameterTiedModel(nn.Module):
    def __init__(self):
        super(ParameterTiedModel, self).__init__()
        self.linear1 = nn.Linear(1, 1)
        # self.linear2 = nn.Linear(1, 1)
        
        # # 参数绑定：使linear2的权重和偏置与linear1的相同
        # self.linear2.weight = self.linear1.weight
        # self.linear2.bias = self.linear1.bias
        
        self.linear1.weight.data[0] = 2.0
        self.linear1.bias.data[0] = 1.0
    
    def forward(self,x):
        # return self.linear2(self.linear1(x))
        return self.linear1(x)
        
shared = ParameterTiedModel()
shared1 = ParameterTiedModel()

# shared = nn.Linear(1,1)
net = nn.Sequential(shared,shared1)

optimizer = torch.optim.SGD(net.parameters(), lr=0.1)


X = torch.tensor([1.0])
Y = torch.tensor([3.0])

loss = net(X) - Y
loss.backward()
optimizer.step()
# 计算更新后的参数 w1, w2
print(net[0].linear1.weight.data,net[1].linear1.weight.data)

可以验证计算结果：

tensor(1.8000) tensor(1.7000)

假设这两层参数是绑定的，可以一层一层计算参数，反向传播计算到第二层时有一个梯度，到第一层时又有一个梯度，都是对同一组参数 (w,b)，这两次计算的梯度应该相加，原因是两次都指明了参数上升最快的方向，这两次方向应该按矢量法则相加：

5.2 参数管理.png|center|600 参数绑定下的梯度计算 （实现代码如下图）

class ParameterTiedModel(nn.Module):
    def __init__(self):
        super(ParameterTiedModel, self).__init__()
        self.linear1 = nn.Linear(1, 1)
        # self.linear2 = nn.Linear(1, 1)
        
        # # 参数绑定：使linear2的权重和偏置与linear1的相同
        # self.linear2.weight = self.linear1.weight
        # self.linear2.bias = self.linear1.bias
        
        self.linear1.weight.data[0] = 2.0
        self.linear1.bias.data[0] = 1.0
    
    def forward(self,x):
        # return self.linear2(self.linear1(x))
        return self.linear1(x)
        
shared = ParameterTiedModel()
shared1 = ParameterTiedModel()

# shared = nn.Linear(1,1)
net = nn.Sequential(shared,shared)

optimizer = torch.optim.SGD(net.parameters(), lr=0.1)


X = torch.tensor([1.0])
Y = torch.tensor([3.0])

loss = net(X) - Y
loss.backward()
optimizer.step()
# 计算更新后的参数 w, b
print(net[0].linear1.weight.data,net[1].linear1.bias.data)

可以验证计算结果：

tensor(1.5000) tensor([0.7000])
总结

参数绑定下的梯度，应该是先当做未绑定的参数，再计算参数梯度结果，矢量相加

参考文献

© 2023 yanghn. All rights reserved. Powered by Obsidian